The Moon Illusion

Why does the rising moon on the horizon look so much larger than it does overhead? And why is the illusion greater at sea than on land? And why is it greater in the city than in the country? And why is it greater if there’s a little ambient light, rather than if it’s pitch dark?

This is a well-known illusion, but the reason why it happens is not as well-known. I didn’t find out until college, in a 300-level class at the University of Arizona called Sensation and Perception. (I’m not certain that was the name of the class, but it was certainly the name of the textbook.)

Yes, It’s Really an Illusion

The first step is to realize that this happens behind your eye, not in front of it. It is not due to atmospheric effects, or an exaggerated elliptical orbit of the moon. The moon does have a slightly elliptical orbit; its distance from us varies by 32,000 miles from closest to farthest point; but at an average distance of 238,900 miles, it’s not enough to account for the illusion, which can transpire during the rising of the moon on a single night (the moon seems to shrink as it rises).

You can demonstrate to yourself that the moon’s distance from us is not changing by holding a ruler at arm’s length when the moon is on the horizon and noticing its apparent diameter on the ruler (about 1/4" for most people). When it’s at its zenith, check its size again. It’s the same. The visual angle it subtends—the image cast on the back of your eye—is the same in both cases.

The Trigonometry of Size Perception

The second step is to realize that this illusion can only happen with an object, like the moon, that is so far away that our binocular vision cannot tell us its distance. Our perception of an object’s size is heavily dependent on our estimate of its distance from us. Conversely, if we know an object’s size, that can help us understand how distant it is from us (like looking down at cars on a road from an airplane window), but this inverse perception of distance seems to be happening at a conscious, cognitive level, not at an unconscious level, with the attendant convincing power that causes an illusion—the perception of something we know to be untrue.

In the diagram below, our perception of the height H of an object is 2Dtan(A/2), where D is the distance from the object and A is the visual angle. The eye’s measurement of the visual angle is always right; it’s really the only thing that one eye by itself can measure.

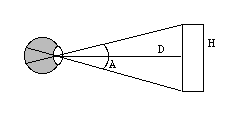
In many cases, D is determined accurately by our binocular vision. But when the object is so far away that there is no binocular disparity, our eye must use monocular cues, hints from the surrounding environment, to make a guess at D. If the guess is wrong, the perception of the object’s size is wrong, in an inverse relationship: if we guess that the object is too far away, it is perceived as larger, and if we guess that it is too close, it is perceived as smaller.

Mathematically, this is clear: if H = 2Dtan(A/2), then tan(A/2) = H/(2D). The quantity (tan(A/2)) won’t change (because the moon is neither actually changing size or distance from us), so if our estimate of D decreases, H must decrease; if our estimate of D increases, H must increase.

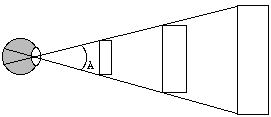
Intuitively, you can imagine your occipital cortex saying, “if it’s that far away, and still looks that big, it must be enormous”; or “if it’s that close, and still looks that small, it must be tiny”. In the diagram below, notice how all three objects, though different actual sizes, create the same size image on the retina. For a given visual angle, perceived size increases with perceived distance.

You Mean It’s Five Whole Miles Away?

Now back to the moon. It’s a whopping quarter of a million miles away and is over two thousand miles in diameter. There’s just nothing in our visual system that is prepared to deal with that kind of distance and size. So first of all, our binocular cues are out of the question. And second, our monocular cues, which are derived from our normal environment, are useless or absent.

A monocular cue is an indication of distance that is derived entirely from the retinal image. You can think of this as the class of depth cues that “work” in a two-dimensional picture or painting: things like vanishing points, perspective, shadows, textures.

When looking at the moon overhead, there are no cues at all, only an image of a white disc. So our eye has some “default” value of the distance D for “unfilled space”. I don’t know what it is, but—it’s less than the perceived distance of the horizon. This is how the whole illusion works, and helps predict what kinds of phenomena exaggerate the illusion.

At sea, for example, the surface of the water out to the horizon provides an excellent monocular cue, giving our occipital cortex a good estimate of the distance to the horizon, about five miles, I think, if you’re in a small boat. This is evidently a large value for D, making us perceive H larger, too. If you are on the deck of a tall ship, or in the crow’s nest, the distance to the horizon should be even greater, making the moon appear even larger.

Suppose you’re in the country, late at night, when the moon rises. Because there is no ambient light with which to view the monocular cues which suggest the distance of the horizon, the eye may have to use its same “default for unfilled space” value, greatly reducing, or even removing, the illusion. On the other hand, if you’re in the city, with uniformly tall street lights and telephone poles providing the same kind of good monocular cues as when you’re at sea, the illusion should be more striking.

This last one I can testify to myself. A few months ago, well after sunset, I was in the city and driving to the country when the moon rose. It looked huge, magnificent. “I can’t wait until I get out of the city to really appreciate this,” I thought. I was at the edge of the city already, so in just a few minutes I was beyond the streetlights—and the moon looked far less impressive. (I know that the moon was able to rise a little during that time, but not much.)

Dispelling the Illusion

If all this is true, then the monocular cues are the key to all of it. Remove those (by driving out of the city, watching the moon rise when it’s pitch dark, etc.) and the illusion goes away. You can force this yourself the next time an amazingly large moon is rising. Grab an opaque piece of paper, punch a small (1/4" or so) hole in it, and peep at the moon through it, so that you can’t see the horizon. Voila! It looks as small and miserable as the moon at its zenith. Now throw away the paper and just enjoy the view.

A question I asked in my perception class was, “what if you were looking at the moon, at its zenith, but up against an enormously tall structure that acted like a vertical horizon?” Nobody knows, because it’s exceedingly difficult to find that kind of surface. Perhaps if you were at the foot of a skyscraper, with the moon appearing to be near its roof. Of course, the skyscraper probably isn’t even a measly mile high, so I don’t know if this would help (as I said, I don’t know what that “unfilled space” value is).

Footnotes

The book is Sensation and Perception, by E. Bruce Goldstein, 3rd edition, from the Wadsworth Publishing Company. The description of the “apparent distance theory”, its challenges, and eventual victory, starts on p. 254. The expanded description in this essay, however, and the accompanying diagrams, are my own.
Data is from Grolier’s 1995 Multimedia Encyclopedia, version 7.0.2, entry on “Moon”.